
Sinusbewegung
Berechnung von Hydraulikzylindern, Oszillationszylindern
Die einfachste harmonische Sinusschwingung einer geregelten Zylinderachse ist ein zyklisches Aus- und Einfahren der Kolbenstange. Aber auch völlig unregelmäßige Fahrprofile lassen sich mathematisch beschreiben, indem man an jedem Punkt eine Sinusbewegung zu Grunde legt.
Die im Produktkonfigurator HäKo (Prüfzylinder >> Hydraulische Auslegung) integrierte vereinfachte Berechnung dient zur Auslegung einer dynamischen Bewegung im Sinusbetrieb. Dabei werden vor allem Zylinderdaten berücksichtigt, weitere systemrelevante Teile wie zum Beispiel Schläuche oder Ventile und deren Leckagen werden nicht mit einbezogen.
Die Sinusbewegung wird durch die Eingabe von Amplitude und Frequenz definiert. Damit ermittelt die Berechnung die jeweiligen Maximalwerte der Bewegung, die aber bei einer sinusförmigen Schwingung nicht gleichzeitig auftreten. So hat zum Beispiel die Geschwindigkeit ihren Maximalwert in dem Moment, in dem der Beschleunigungswert Null ist.
Zur Ermittlung der Zylindergröße ist dies für eine typische Auslegung ausreichend.
Diese Berechnung ersetzt nicht die Simulation des vollständigen Hydrauliksystems, die in besonderen Fällen erforderlich ist, zum Beispiel wenn das System an seine Auslegungsgrenzen kommt.
Die Berechnung dient zur Auslegung einer Bewegung im Sinusbetrieb. Sie umfasst nicht das Verhalten beim Ein- oder Ausschalten der Hydraulikanlage.
Kräfteberechnung
Die Zylinderkraft Fb bei Betriebsdruck ist die Kraft, die im dynamischen Betrieb erreicht wird. Mit Betriebsdruck wird der in der Zylinderkammer tatsächlich herrschende Druck pb bezeichnet, der sich hinter dem Stetigventil einstellt.
Fb = pb • A
mit der wirksamen Kolbenfläche aus Kolbendurchmesser D2K und Kolbenstangendurchmesser d2s
A = π / 4 • (D2K - d2s)
Die Zylinderkraft Fs bei Systemdruck ist die Kraft, die im statischen Betrieb erreicht wird. Mit Systemdruck wird der vor dem Stetigventil herrschende Druck ps bezeichnet, der vom Aggregat zur Verfügung steht.
Fs = ps • A
Dynamische Sinusbewegung
Im dynamischen Betrieb ergeben sich bei einer Sinusbewegung physikalische Zusammenhänge zwischen
- Amplitude +/- x - die tatsächliche Hubbewegung während der Schwingung
- Geschwindigkeit v - die momentane (und während der Schwingung ständig wechselnde) Kolbengeschwindigkeit
- Beschleunigung a - die momentane (und während der Schwingung ständig wechselnde) Kolbenbeschleunigung
- Frequenz f - die zeitliche Folge der Hubbewegung, angegeben als Anzahl Schwingungen pro Zeiteinheit
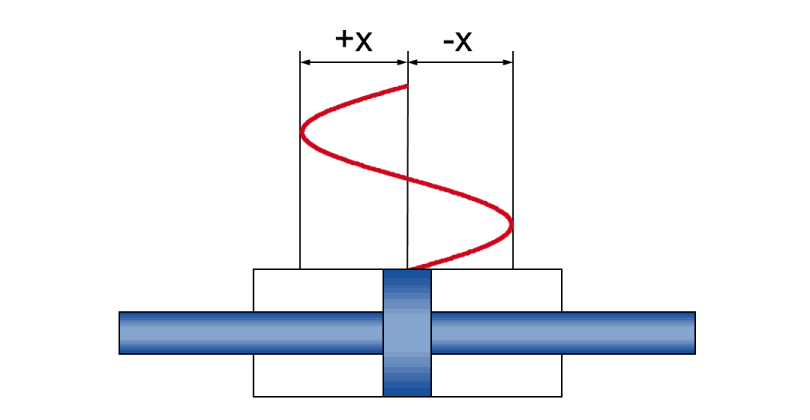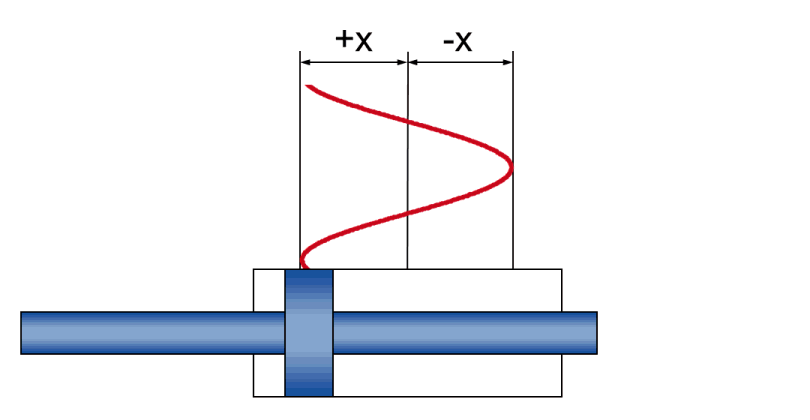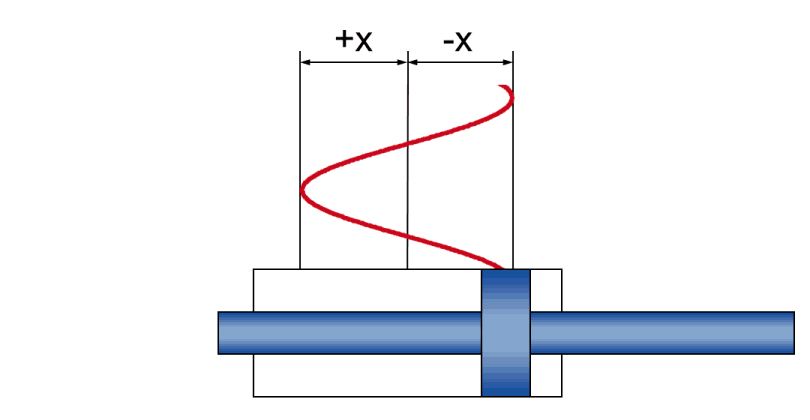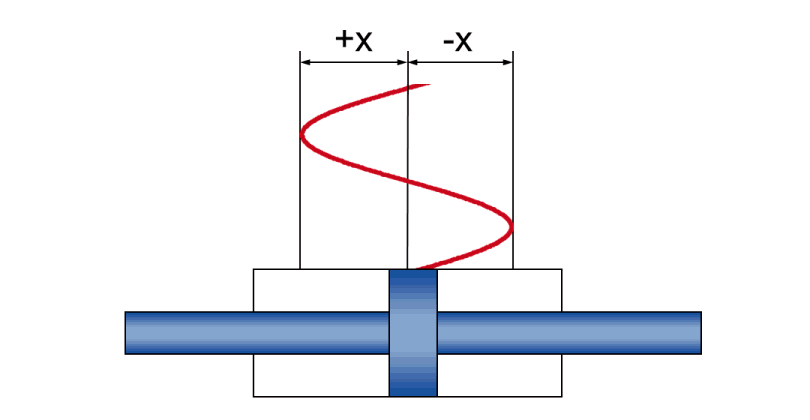
| Maximalwerte |
| v = 2 π f x |
| a = 4 π2 f2 x |
Daraus ergibt sich der für die Bewegung max. erforderliche Volumenstrom Q
Q = v • A
mit der wirksamen Kolbenfläche A
A = π / 4 • (D2Kolben - d2Stange)
und die vom Zylinder zu erbringende Beschleunigungskraft Fa
Fa = m • a
Aus der hier berechneten maximalen Beschleunigung und der bewegten Masse ergibt sich eine Beschleunigungskraft, die der Zylinder aufbringen muss. Die Eigenmasse der Kolbenstange ist im Berechnungsprogramm berücksichtigt, zusätzliche bewegte Massen sind im entsprechenden Feld anzugeben.
Servoventil-Empfehlung
Der Systemdruck ps berechnet sich unter Berücksichtigung des Druckabfalls Δp im Stetigventil zu:
pb = ps - Δp
Der Druckabfall des Stetigventils wird bei Regelventilen üblicherweise mit 70 bar oder 10 bar bei Nenndurchfluss angegeben. Im Betrieb ist dieser aber abhängig vom tatsächlichen Durchfluß.
Das Programm gibt dem erforderlichen Volumenstrom entsprechend einen Vorschlag für den Nenndurchfluss für ein mögliches Stetigventil aus. Dafür wird dann auch der Druckabfall berechnet. Dadurch soll schnell ein Überblick erreicht werden, welche Größenklasse von Ventil erforderlich wäre.
Zum berechneten Volumenstromwert muss der Leckölstrom des Dichtsystems und des Servoventils addiert werden.
Eine genaue Ventilbestimmung und Auslegung bleibt von dieser Auslegung unbenommen.
Weitere Berechnungsformeln zur Auslegung von Hydaulikzylindern:
Berechnungsformeln zur Auslegung von Hydraulikzylindern
Berechnung der zulässigen Ölgeschwindigkeiten
Berechnung der Knickfestigkeit von Hydraulikzylindern
Knickungsfälle Berechnung - Befestigungen von Kolbenstange und Zylinder